LOS CONCEPTOS MATEMÁTICOS NO SE EXPLICAN: SE CONSTRUYEN (I)

Por qué explicar bien no basta (y qué hacer en el aula para que el aprendizaje sea real)

Durante años hemos actuado como si aprender matemáticas fuera, esencialmente, escuchar buenas explicaciones. Si el docente define con claridad, pone ejemplos ordenados y muestra el procedimiento paso a paso, el concepto “debería” quedar aprendido. Cuando no ocurre, solemos buscar el problema en el alumno: no ha atendido, no ha practicado lo suficiente, no tiene facilidad.

Sin embargo, desde hace décadas la psicología cognitiva del aprendizaje es bastante clara en esto: los conceptos no entran en la cabeza por vía directa. Ni se transmiten ni se descargan. Se construyen.

Y esta idea —aparentemente simple— tiene consecuencias profundas para cómo enseñamos matemáticas en Primaria.

Empecemos por desmontar dos ideas equivocadas muy habituales:

❌ Si explico bien, el alumno comprenderá.

❌ Si el alumno comprende, es porque lo ha descubierto.

Como sabéis los que seguís este blog habitualmente, ninguna de las dos se sostiene desde la evidencia.

Un concepto matemático no aparece automáticamente cuando el docente lo define con claridad, ni aunque lo explique despacio, con buena letra y ejemplos “claros”, pero tampoco aparece por generación espontánea cuando el docente se retira y propone actividades “abiertas”.

El concepto matemático se construye cuando el alumno integra múltiples experiencias y detecta regularidades entre ellas. La idea clave es esta: Cada nueva experiencia se interpreta a través de las anteriores.

Esto significa que el aprendizaje no empieza en la explicación, sino en lo que el alumno ya trae consigo (una vez más, los conocimientos previos). Eso significa que el aprendizaje depende de:

• qué experiencias previas tiene el alumno,
• cómo están organizadas,
• qué regularidades ha podido detectar.

La función del docente no es desaparecer, sino diseñar esas experiencias, apoyando su explicación en esquemas previos; si esos esquemas son pobres, el concepto que se construye posiblemente acabe siendo frágil.

Veamos el desarrollo de una sesión estándar desde un punto de vista docente: primero explica el concepto, da ejemplos, los alumnos practican y finalmente evalúa. Esta secuencia suele ser una de las más lógicas.

Pero… ¿Qué ocurre desde el punto de vista del alumno? Desde su punto de vista, pueden estar ocurriendo cosas bastante distintas: primero solo reconoce patrones superficiales, luego imita pasos, responde practicando ejercicios muy parecidos entre sí y finalmente se bloquea cuando algo cambia en el planteamiento de la pregunta o el contexto. Parecía que el alumno había aprendido. Pero lo que ha aprendido es a reconocer situaciones familiares, no a comprender el concepto.

Qué significa realmente “construir un concepto”

Construir un concepto matemático implica desarrollar un esquema mental: una estructura que permite reconocer una situación, entender qué está pasando y decidir qué hacer, incluso cuando el contexto cambia. Por tanto, un esquema no es una definición verbal, ni un procedimiento memorizado, ni una lista de pasos.

Un esquema es una red de relaciones. Y las redes no se improvisan, sino que se construyen cuando el alumno:

• ve variación,
• compara situaciones,
• detecta patrones,
• se equivoca,
• contrasta,
• explica.

Sin eso, lo que queda es un envoltorio sin contenido significativo. Ahora bien, aquí conviene ser muy claros: Construcción no equivale a descubrimiento autónomo. Desde la psicología cognitiva sabemos que el descubrimiento puro sobrecarga la memoria de trabajo, favorece aprendizajes superficiales y beneficia solo a quien ya tiene esquemas previos. Por eso, cuando decimos que el alumno “construye” el concepto, lo que estamos diciendo es que el docente debe guiar cuidadosamente esa construcción. Vayamos a explorar diversos ejemplos.

FRACCIONES Y PIZZAS

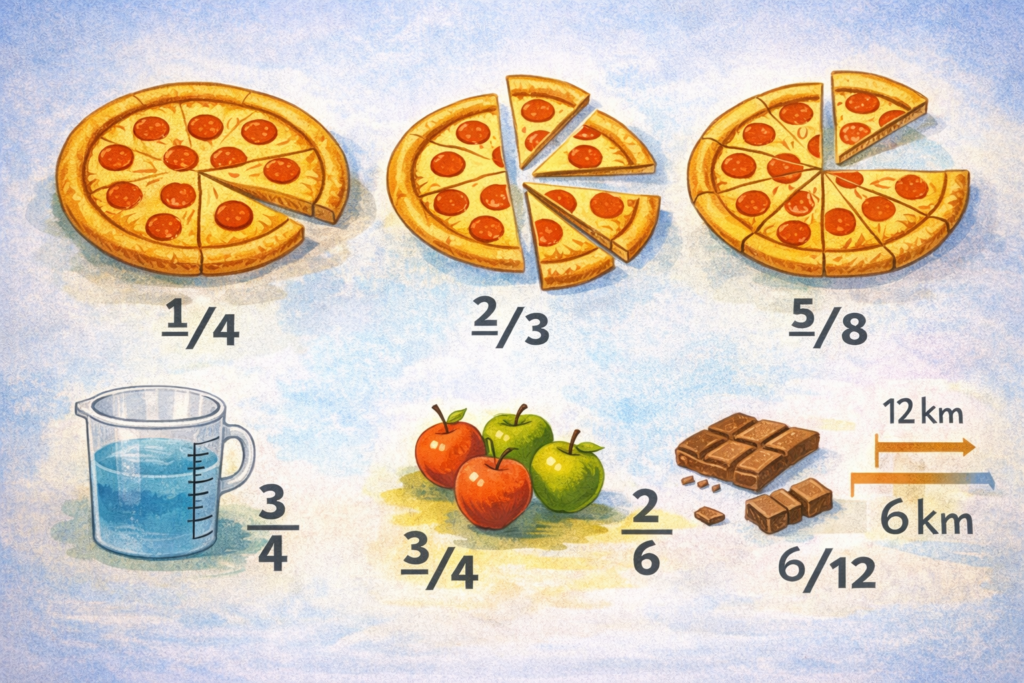
El ejemplo de la fracción como “parte de una pizza” es casi universal. Y no es malo en sí mismo. El problema es cuando se convierte en el único marco de experiencia. El alumno puede haber hecho decenas de ejercicios… y aun así no reconocer la fracción cuando desaparece la pizza.

¿Qué aprende el alumno?

• que una fracción es algo redondo,
• que se corta,
• que suele repartirse,
• que tiene sentido “visual”.

Cuando la fracción aparece como:

• 3/4 de litro,
• 2/3 de una distancia,
• una razón entre cantidades,
• una fracción mayor que 1,

el alumno se pierde. ¿Por qué? Porque no ha construido el concepto, ha construido una imagen. Entonces… ¿cuál es el papel aquí del docente? Diseñar la sesión seleccionando ejemplos distintos desde el inicio, mostrando explícitamente qué es lo común entre todos ellos, señalando qué cambia y qué no. No esperamos a que el alumno «lo descubra solo», sino que se le guía para que pueda verlo.

Respecto a la variedad real de ejemplos, las actividades tienen que ir mucho más allá de un simple cambiar números. Uno de los errores más frecuentes en matemáticas es confundir repetición con variación. Cuando nuestro alumnado practica con 20 ejercicios iguales solo cambian los números, pero no la experiencia cognitiva.

La investigación es clara: los conceptos se forman cuando el alumno aprende qué pertenece al concepto y qué no, por lo que en nuestro diseño debemos exigirnos variedad intencional y no acumulación mecánica. Veámoslo ahora con un ejemplo a partir de trabajar el concepto de número.

Ejemplo: el concepto de número

Vamos a por un enfoque clásico para trabajar el número en clase en infantil o primer ciclo de primaria: contamos objetos, decimos la serie numérica y asociamos la cifra con la cantidad que le corresponde. Sin renunciar a ello, limitar la construcción del concepto numérico a estas tres actividades puede llevar al alumno a pensar que el número solo existe cuando hay cosas visibles. Además, cuando luego aparezca el número 0, trabajemos los números negativos, números grandes no representables o números como medida, el concepto va a tambalearse.

Para evitar eso, y construir el concepto de número de manera más profunda, exigimos experiencias como:

• comparar cantidades sin contar,
• estimar,
• ordenar,
• medir,
• usar números como posición, como cantidad y como etiqueta.(*)

No se trata tanto de adelantar contenidos, sino de ensanchar el concepto. Nada de esto surge por descubrimiento espontáneo. El docente decide qué experiencias ofrecer y en qué secuencia. Eso es instrucción directa basada en evidencia.

(*)

El concepto de número se construye cuando el alumno aprende a distinguir estas funciones, no cuando las ve por separado en fichas limpias y ordenadas. ¿Qué tal si intercalamos…? Así, en una misma sesión:

• contamos objetos (cantidad)
• hablamos de posiciones en una fila (posición)
• usamos números como nombres (etiqueta)

Y después preguntamos: “Aquí, ¿el número nos dice cuántos, dónde o quién?” Ahí es donde aparece el pensamiento matemático.

A partir de «Psicología del aprendizaje de las matemáticas» de R. Skemp. Ediciones Morata, 1980.